Distributed Orthogonal Slicing for Load Balancing of Large Spatial Datasets
Imagine you have N objects placed in a multidimensional space, stored across a distributed network of C compute nodes. The problem is simple:
- how to divide the universe in such a way that each compute node gets an equal number of objects
N/C? and - how to ensure that objects of each compute node are as close as possible to each other? and
- how to ensure that the regions of overlap of objects across compute nodes is none or minimal?
This is a very common problem setup, and a problem of high importance on large-scale scientific problems. The main rationale is that a good spatial decomposition should allow for close objects to be stored on the same memory region (compute node), such that internode dependency (communication) is reduced.
The simplest spatial decomposition algorithms perform an orthogonal spatial decomposition (slicing). On a 2D space, there are several slicing alternatives:

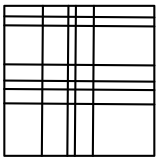

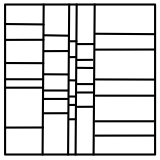
A small note on efficiency. If you pick the slicing layout 1, then you would incur in a lot of duplication of objects when objects are not points in space but have volume, and when there is a high number of slices. Layout 2 works better by reducing cloning, yet it does not guarantee an accurate spatial decomposition. Layouts 3 and 4 are similar, but layout 4 outperforms layout 3 in parallelism. This is because layout 3 performs a tree-based recursive bisectional decomposition (ie at every level of the tree it computes 2 slices), while layout 3 peforms several slices at once for each of the 2 dimensions.
The following table details the complexity of each algorithm (we assume sorting with average complexity \(n log n\):
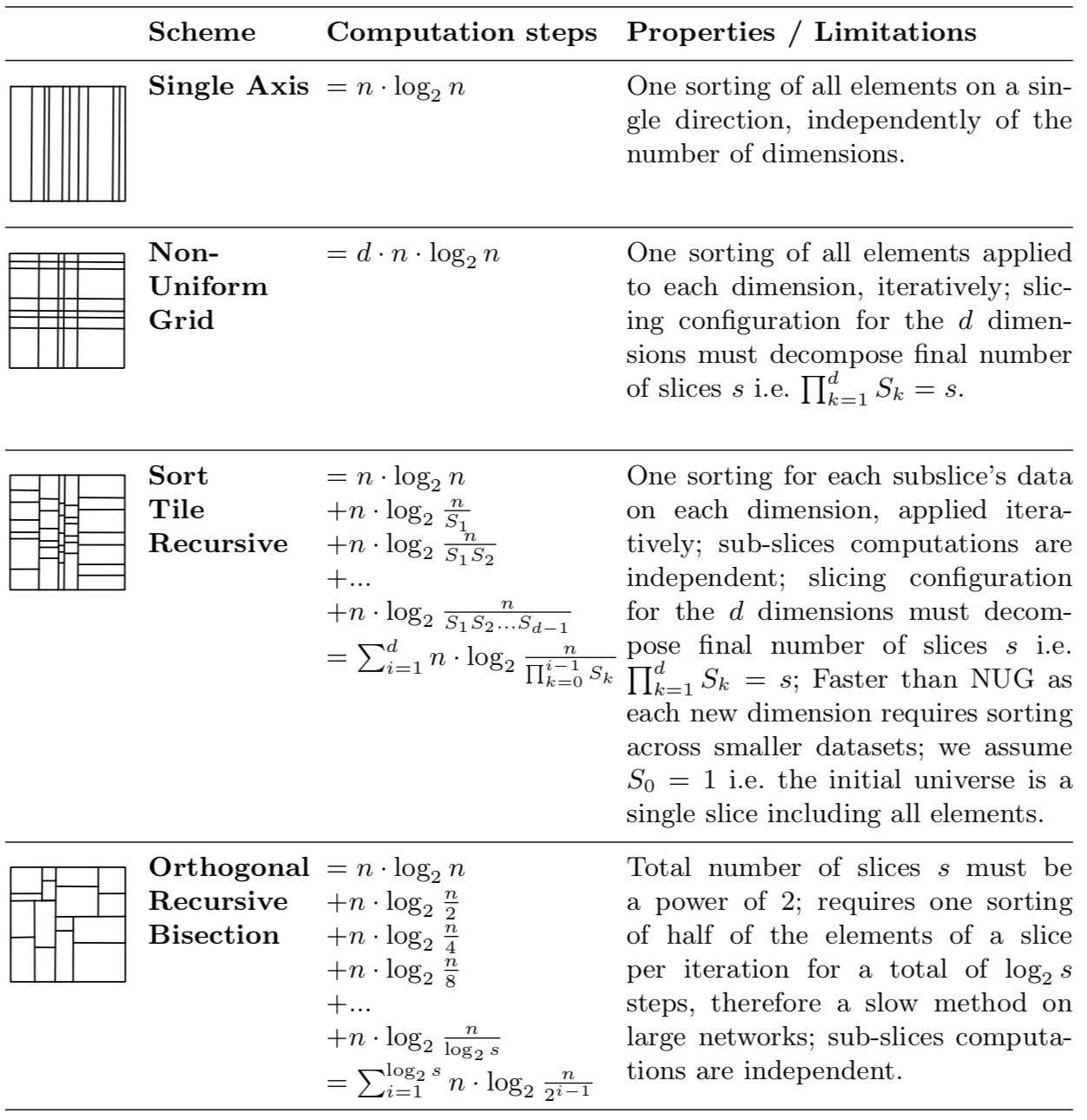
Accross all slicing layouts possible, the (3) is the most efficient and guarantees low data duplication, allows for accurate slicing, and requires only D (dimensions) recursive iterations, independently of the number of compute nodes (contrarily to (4)). However, its implementation on a distributed memory environment is not trivial. Possible options are:
- A histogram/binning algorithm that clusters elements in spacial bins and uses the number of elements per bin as a metric used on the slicing;
- A method that performs serial slicing in one compute node that holds only a sample of the date, and uses the slicing from the sampled dataset as the slicing of the final dataset;
Distributed Slicing via Sort-Balance-Split
A technique I published on this paper, called the Sort-Balance-Split (SBS), implements a parallel multi-dimensional slicing based on the previous algorithm. The algorithm follows three steps:
- The sorting step performs a distributed sorting operation of all elements on a given dimension. Distributed sorting algorithm was covered in depth in my previous post;
- The load balancing step equalizes the number of elements across compute nodes, while respecting the initial sorting;
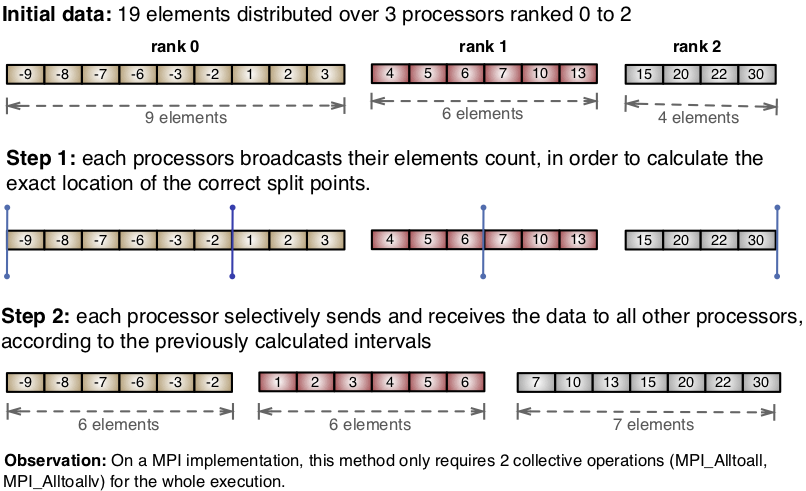
- The splitting step creates smaller networks from subsets of the ranks from the main network. We will call these subnetworks.

The three steps explain the name Sort-Balance-Split. We perform this SBS algorithm at every level recursively, where each level operates on the subnetworks that are created from the split step.
This method has several advantages compared to existing methods, while delivering an efficient execution: (1) a fixed complexity due to the number of communication steps being fixed for any network and input size; and (2) accurate spatial decomposition, ie not approximated.
A sample application of the algorithm on a 2D universe of 16 shapes distributed across 4 compute nodes (ranks) is presented below:
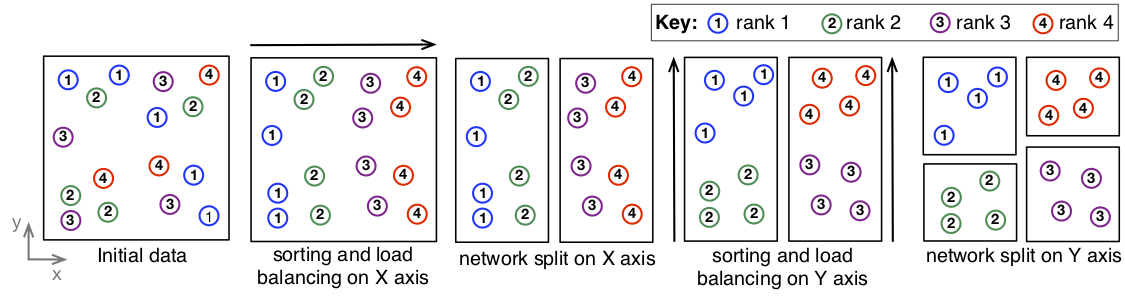
From left to right:
- Initial data layout;
- The inital sorting operation will sort all elements on the first (X) dimension, without caring about the other coordinates. Data is load balanced on the X axis, so that each rank holds 4 shapes;
- A network split divides the initial problem of 16 shapes across 4 nodes on a single network, into a proble of 8 objects on 2 networks of 2 nodes each;
- Each network performs a distributed sort of its objects on the next axis (Y), and balances the workload;
- Final data layout;
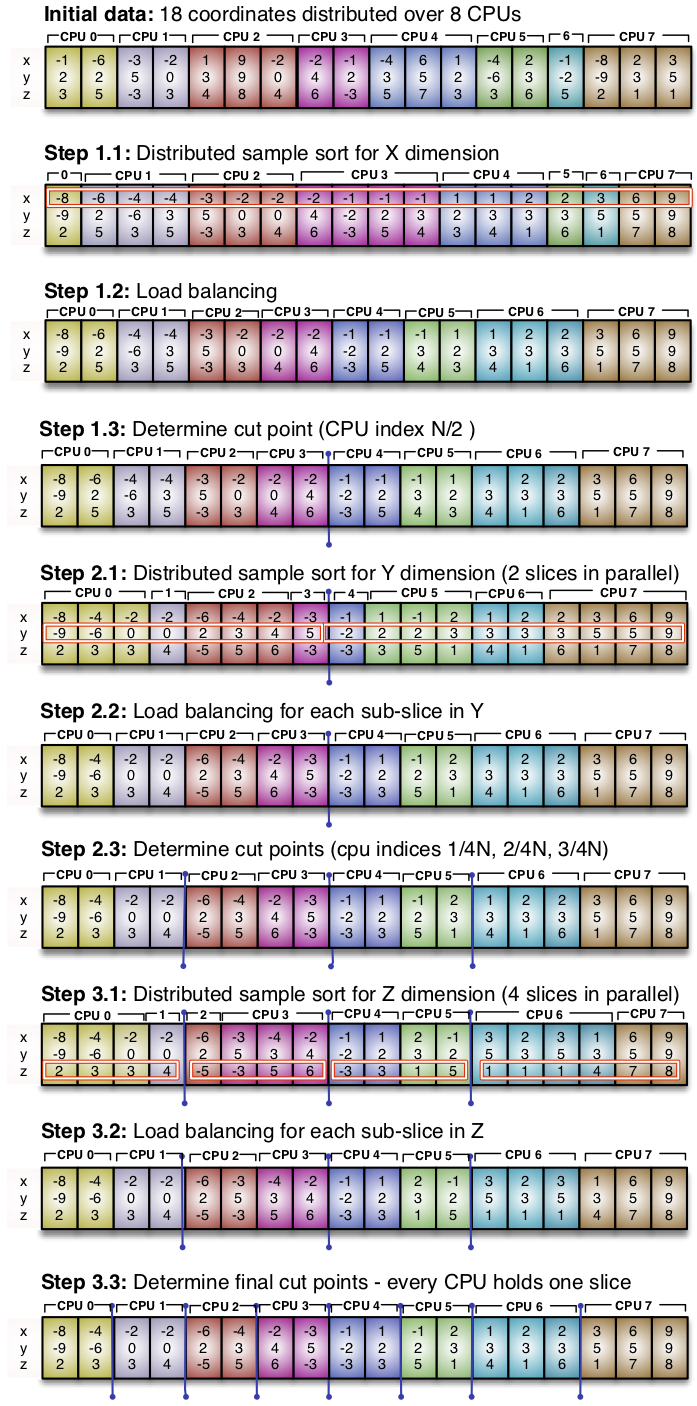
Here is another illustration of the same problem, on a 3D universe, now emphasizing the memory layout across nodes:
And here is an application of a distributed slicing to the N-particles problem, enabling one to simulate cosmic activity such as the Big Bang, and several times winner of the Gordon Bell Prize for Scientific Computing. And an application to a small network of neurons. Enjoy the view.


For limitations, benchmarks and a more thorough analysis of the problem, check the original publication.
For the C++ code implementation, download slicing.tar.gz.